SHM

 Simple Harmonic Motion

Notes

A very common type of 

periodic motion

 is called 

simple harmonic motion (SHM)

. A 

system

 that oscillates with SHM is called a 

simple harmonic oscillator

.

Simple Harmonic Motion

In simple harmonic motion, the acceleration of the 

system

, and therefore the net 

force

, is proportional to the 

displacement

 and acts in the opposite direction of the 

displacement

.

A good example of SHM is an object with mass m$m$ attached to a spring on a frictionless surface, as shown in Figure 15.2.2$\mathrm{15.2.}2$. The object oscillates around the 

equilibrium position

, and the net 

force

 on the object is equal to the 

force

 provided by the spring. This 

force

 obeys Hooke’s 

law

 F_s = −kx, as discussed in a previous chapter.

If the net 

force

 can be described by Hooke’s 

law

 and there is no damping (slowing down due to 

friction

 or other nonconservative forces), then a 

simple harmonic oscillator

 oscillates with equal 

displacement

 on either side of the 

equilibrium position

, as shown for an object on a spring in Figure 15.2.2$\mathrm{15.2.}2$. The maximum 

displacement

 from 

equilibrium

 is called the 

amplitude (A)

. The 

units

 for amplitude and 

displacement

 are the same but depend on the type of 

oscillation

. For the object on the spring, the 

units

 of amplitude and 

displacement

 are meters.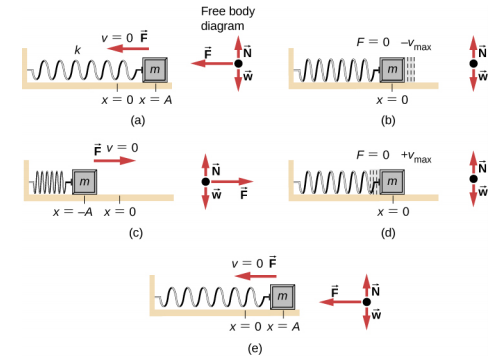

Figure 15.2.2$\mathrm{15.2.}2$: - An object attached to a spring sliding on a frictionless surface is an uncomplicated 

simple harmonic oscillator

. In the above set of figures, a mass is attached to a spring and placed on a frictionless table. The other end of the spring is attached to the wall. The 

position

 of the mass, when the spring is neither stretched nor compressed, is marked as x = 0 and is the 

equilibrium position

. (a) The mass is displaced to a 

position

 x = A and released from rest. (b) The mass accelerates as it moves in the negative x-direction, reaching a maximum negative velocity at x = 0 . (c) The mass continues to move in the negative x-direction, slowing until it comes to a stop at x = −A . (d) The mass now begins to accelerate in the positive x direction, reaching a positive maximum velocity at x = 0 . (e) The mass then continues to move in the positive direction until it stops at x = A . The mass continues in SHM that has an amplitude A and a period T. The object’s maximum speed occurs as it passes through 

equilibrium

. The stiffer the spring is, the smaller the period T. The greater the mass of the object is, the greater the period T.

What is so significant about SHM? For one thing, the period T$T$ and frequency f$f$ of a 

simple harmonic oscillator

 are independent of amplitude. The string of a guitar, for example, oscillates with the same frequency whether plucked gently or hard.

Two important factors do affect the period of a 

simple harmonic oscillator

. The period is related to how stiff the 

system

 is. A very stiff object has a large 

force constant (k)

, which causes the 

system

 to have a smaller period. For example, you can adjust a diving board’s stiffness—the stiffer it is, the faster it vibrates, and the shorter its period. Period also depends on the mass of the oscillating 

system

. The more massive the 

system

 is, the longer the period. For example, a heavy person on a diving board bounces up and down more slowly than a light one. In fact, the mass m and the 

force

 constant k are the only factors that affect the period and frequency of SHM. To derive an equation for the period and the frequency, we must first define and analyze the equations of motion. Note that the 

force

 constant is sometimes referred to as the spring constant.